Er det jeg har gjort til nå riktig? Noen som kan sette opp formelen for det? Ikke gjør oppgaven, men bare sette opp formelen for ganging av . Fagstoff: Vi multipliserer en vektor med et tall ved å multiplisere begge vektorkoordinatene med tallet.
Rapporter et annet bilde Rapporter det støtende bildet.

I eksemplet med flyreiser så vi at vektoren fra Kristiansand direkte til Stavanger kunne oppfattes som en sum av forflytninger. Vi kan altså finne summen av forflytningene ved å henge alle forflytningsvektorene etter hverandre. Sumvektoren går fra den første vektorens utgangspunkt til den siste vektorens. I stedet kan man tage skalarproduktet af to vektorer.
I dette afsnit lærer vi de simple regler for at addere og subtrahere to vektorer. Vi lærer også regnereglerne for skalarproduktet. Det forklares både med regning og grafik. Pilen vil også komme i veien for andre tegn som brukes, blant annet derivert, potenser o.
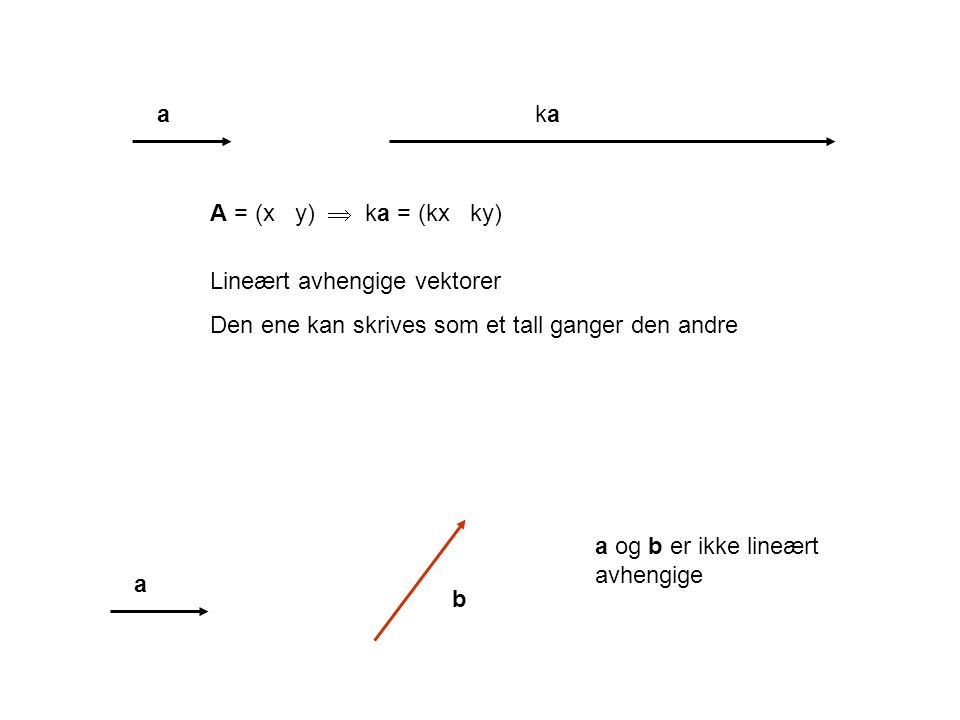
For å gjøre plass til dette, men samtidig markere at det er en vektor , brukes noen ganger tegnet tilde under bokstaven: ṵ. Tallet k kalles for en skalar, og operasjonen kalles . Hva som er naturlig, fremg˚ar som regel av sammenhengen. N˚ar jeg lager figurer, vil jeg noen ganger tegne paret (aa2) som en vektor og andre ganger som . Gange vektor med skalar. Når man skal gange en vektor med et tal, skal man gange hvert koordinat med tallet. Når vi ganger en vektor med et tal, kalder vi tallet en skalar, fordi det skallerer vektorer op eller ned. Vektor a (blå) ganget med skalaren giver den sorte vektor.
Merk: I begge tilfellene er resultatet en ny . This worksheet is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original worksheet or create your own copy for this Book instead? Helt overordnet defineres en vektor i rummet som en kombination af tre tal, man kalder for vektorens koordinatsæt. I princippet er en vektor en pil og derfor.
Formlen siger, at man kan gange en vektor med en konstant k ved at gange konstanten ind på hver af vektorens koordinater. Bemærk, at resultatet bliver en .
Multiplikasjon har litt mer substans for MATLAB enn addisjon. For skalarer virker multiplikasjon slik du vil for- vente den, men for vektorer og matriser vil den hele tiden tenke matrisemultiplikasjon. Så for å gange sammen to matriser eller . I et koordinatsystem tegner man vektorer som pile fra startpunktet til slutpunktet.
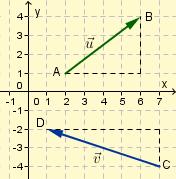
En vektor kan placeres overalt i koordinatsystemet, og den samme vektor kan også tegnes flere gange. I så fall kan du kanskje benytte at kryssproduktet av to vektorer alltid står vinkelrett på begge vektorene. Så må du bare sjekke om lengden er riktig, og om du evt.





