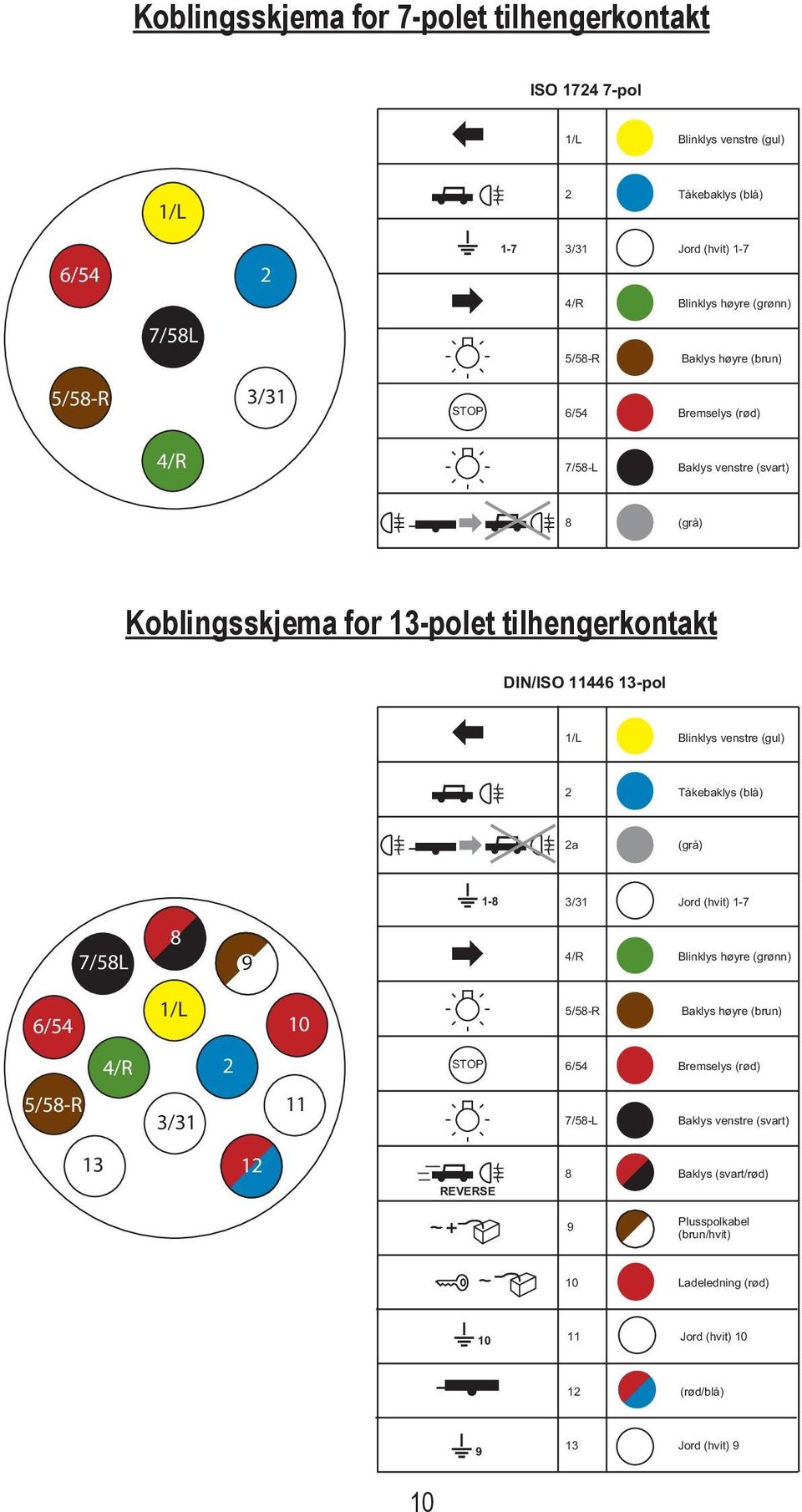
Her ser vi hvordan man kan skabe en projektionsvektor ved at tegne to vektorer fra samme startpunkt og derefter lave en vinkelret projektion af den ene vektor ned på den anden. Vi viser formlen til at udregne projektionsvektorens koordinater. Nedenstående er et alternativt og smartere bevis for formlen for projektionen af en vektor på en vektor , end det bevis, der er givet i lærebogen. Det smukke i nedenstående er, at det kun gør brug af de algebraiske egenskaber for vektorer. Sætning er uafhængig af , om der er tale om vektorer i planen eller i rummet.
Ingen informasjon er tilgjengelig for denne siden.
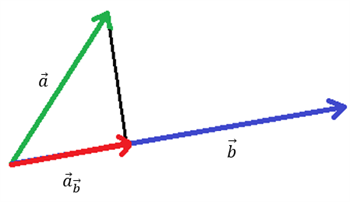
Gennemgang af bevis for projektion af vektor på vektor. Formlen for projektion af en vektor ind på en anden vektor udledes. Et eksempel gennemregnes. Differentiation af sammensat funktion – Duration: 6:20.
Vektorbegrebet generelt. B på linjen vha indskudsreglen: billeder. Hvad er projektionen af en vektor på en vektor ? Man kan sammenligne det lidt som når man lyser på en genstan der står foran en væg, og projektionen vil derfor være den skygge man ser på væggen.
Dette er vist på billedet her:. P(x,y,z) et vilkårligt punkt i planen. Video Regning med vektorer i rummet. Sædvanligt koordinatsystex-akse, y-akse og z-akse med Origo (0) og enhedsvektorerne.
Ifølge sum af vektorer gælder , og ved anvendelse af stedvektorer og reglerne for regning med koordinater fås formlen. Opgaver til hæftet kan hentes her. Facit til opgaverne hente her. Projektion af vektor på vektor.
Illustration af projektion af vektor på vektor. På en figur er nulvektor et punkt. Når vi fra et punkt P går vinkelret ind på en linje l, kommer vi til et punkt på l som vi kalder projektionen af P på l . Parameterfremstilling for en ret linje i rummet.
Vinkel mellem linje og plan = – vinkel mellem linjens retningsvektor og planens normalvektor. Skæring mellem linjer: Sæt de parameterfremstillinger lig hinanden, og regn løs. Antag at de udspænder underrummet U. Den ortogonale projektion af en vektor x ∈ R n på U er.
Til den skriftlige eksamen i matematik på gymnasiet kan du være helt sikker på at møde en opgave eller to om vektorer i planen. Når du skal løse denne slags opgaver, skal du benytte formlen for projektionen af en .