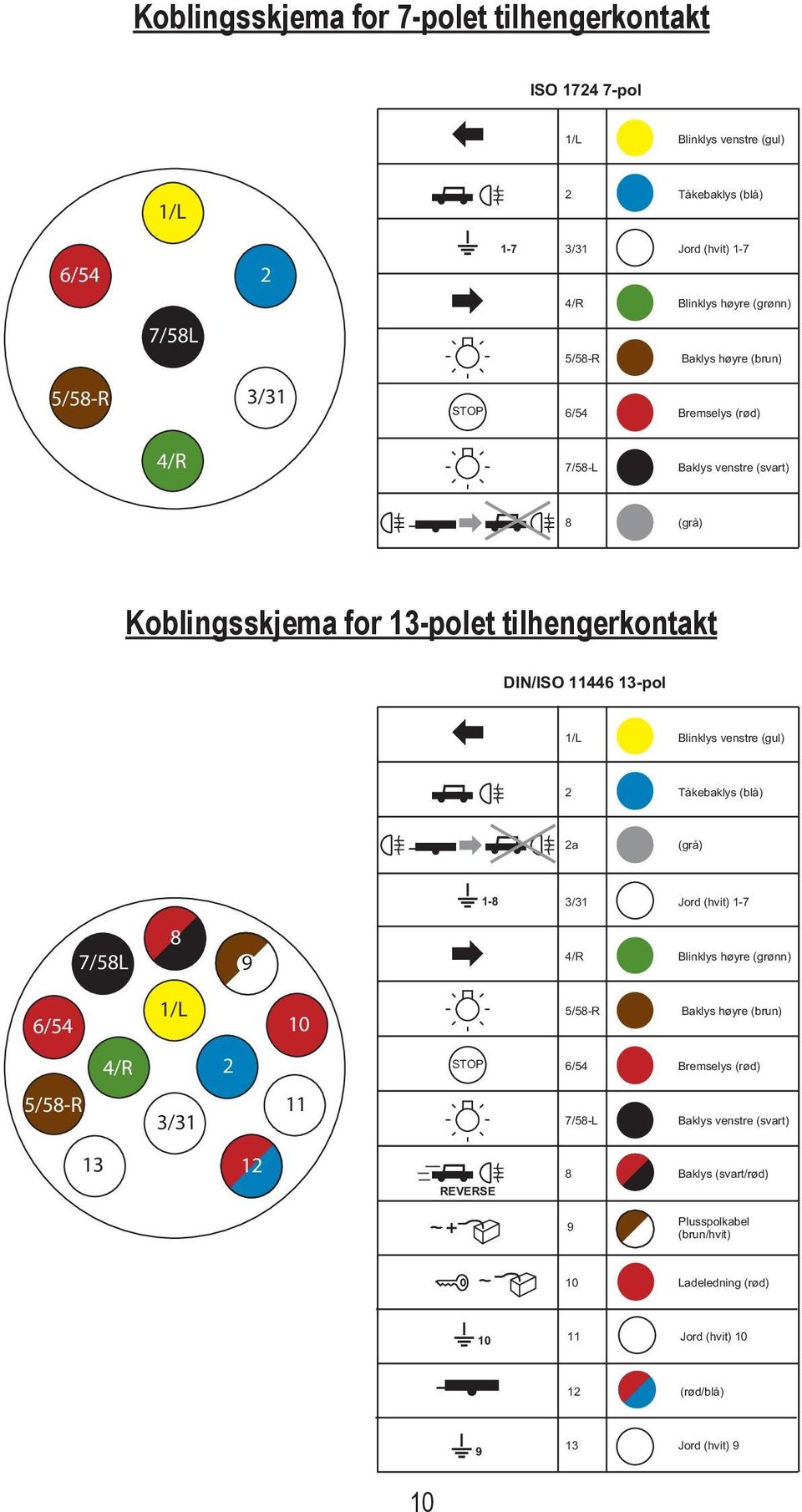
Et parallellogram er en firkant, altså en figur innenfor geometri, med fire sider. Om man da kjenner lengden av to sider og vinkelen mellom dem, kan man beregne arealet av parallellogrammet ved hjelp av sinus. Her er sidelengdene a = c og b = d. For vinklene gjelder det at ∠ u = ∠ w og ∠ v = ∠ x. Parallellogrammet delt opp i to like store trekanter med høyden h og grunnlinjen g.

For å kunne regne ut arealet av et parallellogram, må vi kjenne én side og høyden på denne siden. Arealet til parallellogrammet er . Den siden som hører sammen med høyden kaller vi grunnlinja, akkurat som i trekanter. Se hvordan man udregner omkreds og areal for et parallelogram. Givet et parallelogram som ovenstående vælger man en af dets sider som grundlinje (g på figuren). Man trækker dernæst en . Areal og omkrets av et parallellogram.
Sidekantene er parvis like lange.
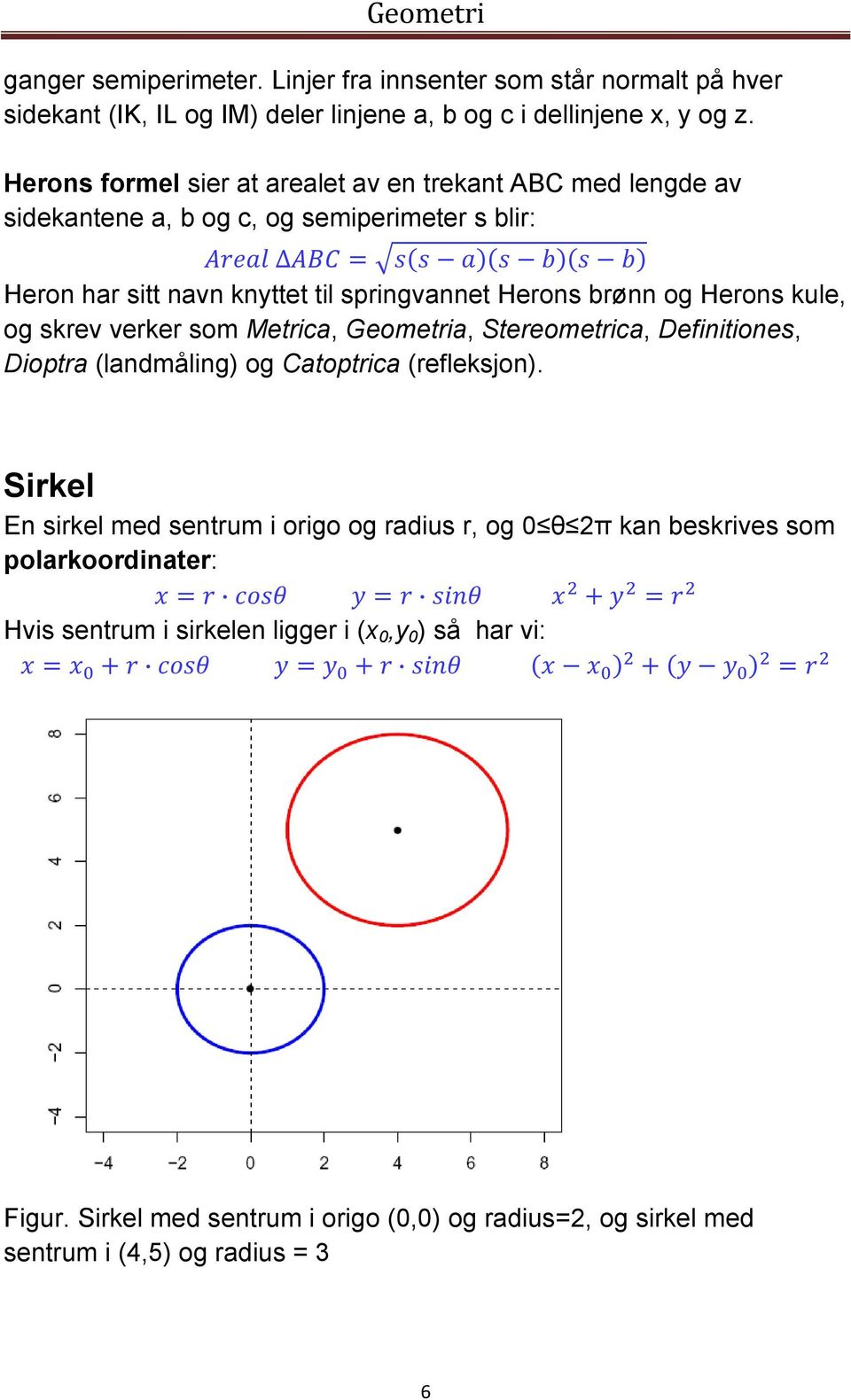
Motstående vinkler er parvis like store. Diagonalene i et parallellogram deler hverandre på midten. Alle parallellogram er også trapes. En delmengde av parallellogram er rektangler, hvor . I dette afsnit vil vi gennemgå, hvordan man beregner arealet af forskellige geometriske figurer. Vi starter med rektanglet og bevæger.
Der gennemgås rektangel, retvinklet trekant, trekant, parallelogram , trapez og cirkel. Lad os nu se, hvorfor den formel ser ud som den gør. Vi kan inddele trapezet i to . Ingen informasjon er tilgjengelig for denne siden.
Hva med parallellogram, rombe og trapes? Du kan sammenligne dine formler med formlene i skjemaet nedenfor. Ved utregning av areal av en trekant tar man utgangspunkt i formelen. Hvorfor er det slik at man må dele på 2? Alle firkanter kan deles inn i to trekanter med liket stort areal. I det här avsnittet undersöker vi hur vi kan beräkna omkrets och area för ett antal vanligt förekommande geometriska figurer.
En triangel som inte är rätvinklig följer samma formel. Däremot identifieras höjden enligt exempelvis följande figur, där linjen som definierar höjden möter basen i en rät vinkel: Omkrets Area _02 . Et parallelogram er en firkant og dets modsatte sider er parallelle og har samme længde, tilstødende sider danner ikke en ret vinkel. Højder er perpendikulære afstande mellem to . Et punkt markeres med et kryss. Punktet P kan markeres slik: Punkt 1. Linjen m har uendelig utstrekning, den fortsetter i begge retninger.
Linjestykket AB ligger på linjen n. Linjen n er uendelig lang, men linjestykket AB har en målbar lengde. Linjen o er uendelig lang, det er også linjestrålen som slutter i C. I kvadrater er lengden og bredden den samme. I rektangler er lengden og bredden forskjellig. Mangler: parallelogram Kolorit 6. Q Det kan være besværligt at bestemme areal af trekanter ved at dele op eller tegne rektangler uden om. Derfor skal l prøve at finde en formel , der kan bruges til at bestemme arealet af alle trekanter.
Klip to ens trekanter som vist, og sæt . Men I kan også udvikle en formel , som gør det hurtigere at finde arealet. På billedet øverst er der to kongruente trapezer. Som I kan se, kan de to trapezer tilsammen danne et parallelogram. Undersøg, om to kongruente trapezer altid kan danne et parallelogram. Hvad er arealet af parallelogrammet øverst?
Og rektanglets lengde og bredde tilsvarer det opprinnelige parallellogrammets grunnlinje og høyde.