En likesidet trekant er en trekant med alle sidene like lange og alle vinklene er grader. Dette er også en type likebeint trekant. På grunn av dens omfannende symmetri blir den også . Sidenes lengde er det ene.
Du har nå en likesidet trekant. Vanligvis feller man ned en normal ved å bruke en bue og merke av to punkter, men her kan vi bruke samme passeråpning som gir punktene A og B.
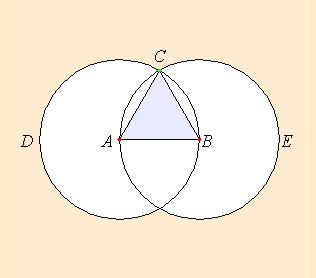
foten for høyden, er midtpunktet: to kryssende buer fra A . En trekant hvor alle sidene er like lange kan du konstruere på følgende måte. Så tar du passerspissen i hjørne A og velger hvor lange sider trekanten din skal ha (mål åpningen på passeren din). Hvordan regner jeg ut arealet, hva er formelen? Likesidet trekant er en trekant der alle sidene er like lange. Alle vinklene i en likesidet trekant er like store, hver av dem er 60°.
I en likesidet trekant er alle sidene like lange og alle vinklene er °. Legg merke til at dersom man halverer en av sidene i trekanten dannes to trekanter som begge er 30°, 60° og 90°. I en likebent trekant er to sider like lange, og de to vinklene på grunnlinjen er like store.

Hvis vi vet en vinkel i en likebent trekant, kan vi finne de andre. Normalen fra toppen ned på grunnlinjen (høyden) i en likebent trekant,. Vi skal se på sammenhengen mellom sida i en lik. Creative Commons license icon. Matematikk Vg2P (Course).
Copyright and Rights to use. Sal beviser at vinkler i likesidede trekanter er kongruente (og derfor måler alle grader), og omvendt. This worksheet is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original worksheet or create your own copy for this Book instead?
Trekant der alle sider , og dermed også alle vinkler, er like store. Hver vinkel er 60° (seksti grader). Ordet trekant kommer av to latinske ord som betyr tre respektive hjørner og vinkel. Eksempel: likesidettrekant. Ingen informasjon er tilgjengelig for denne siden.
Oppskrift, likesidet trekant. Sirkelen vi tar utgangspunkt i har en radius på og en diameter på 2. Ta utgangspunkt i en sirkel. Finn sentrum i sirkelen.

Brett inn et sirkelsegment slik at sirkelbuen ligger inntil sentrum av sirkelen. Den nye sirkelbuen begynner der den foregående .





