Gå til Konvertering mellom polare og kartesiske koordinater – Et diagram som viser forholdet mellom polare og karteiske koordinater. Bufret Lignende Dette systemet er nesten entydig, det eneste unntaket er sentrum C, som er gitt ved koordinatene (v) for en hvilken som helst vinkel v. Utenfor C er koordinatene entydig. Vi kan komme fra det kartesiske koordinater til polarkoordinater ved enkle regneoperasjoner.
Kalkulus: Komplekse tall. Regneeksempler (del 2): Fra kartesiske.
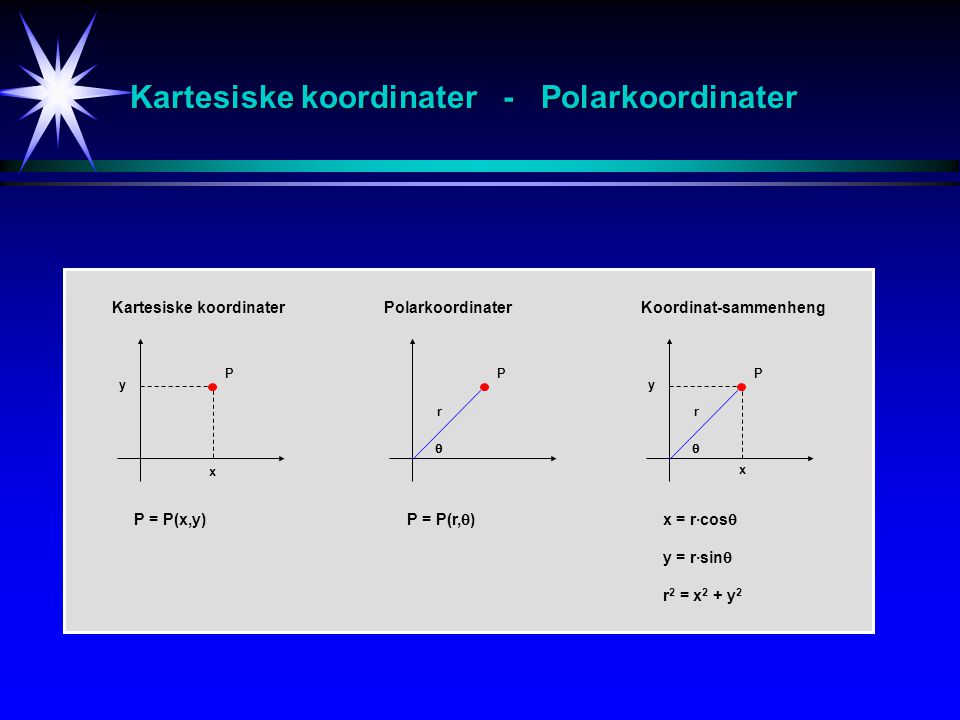
Vi har gitt skalarfeltet β(x, y) = xy i kartesiske koordinater. For polarkoordinater (r, θ) og kartesiske koordinater (x, y) har vi sammenhengen x = r cosθ og y = r sinθ. Gradientvektoren i kartesiske koordinater : ∇β = ∂β. I funksjons-artikkelen om representasjonsformer diskuterte vi det rettvinklede, kartesiske koordinatsystemet som er det vi bruker til vanlig. I en del sammenhenger kan det imidlertid være praktisk å bruke et annet koordinatsystem , polarkoordinater.
I stedet for å angi et punkts x– og y- koordinater angir vi da . Oppgave 1: Følgende punkt er gitt i polarkoordinater. Plasser dem i et koordinatsystem.
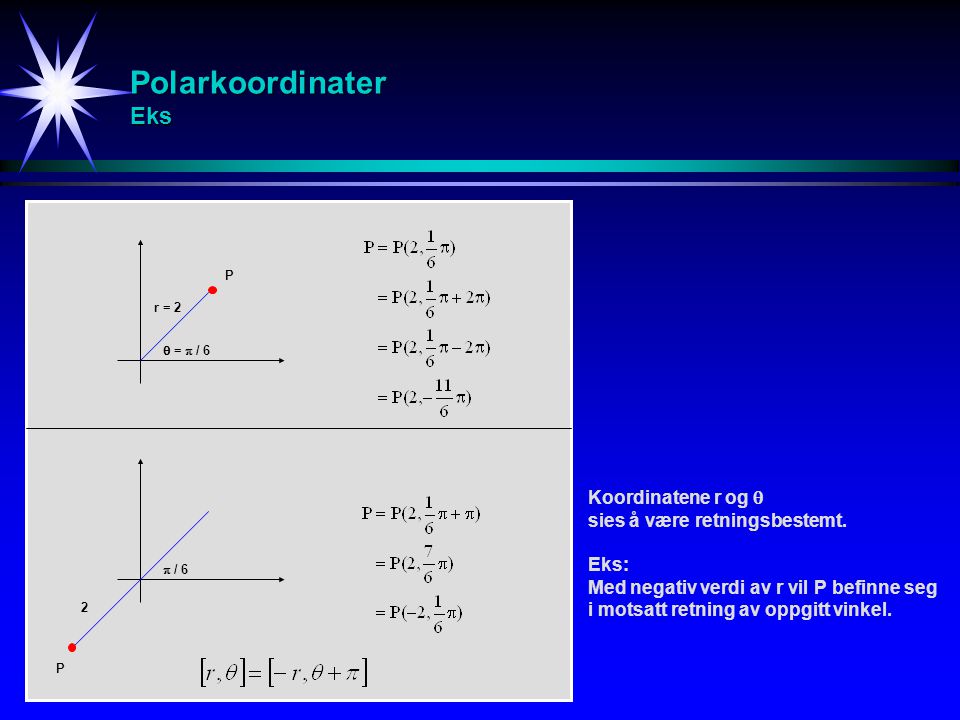
Nå vet ikke jeg hva kartesiske koordinater er, men fasitsvaret på oppgaven er at skjæringspunktene er ( 0) og (2^(5), 2^(5)) (Skrev 2^(5) i stedet for kvadratroten av 2. Polarkoordinater er en annen måte å uttrykke punkter i planet på enn vanlige kartesiske koordinater. I polarkoordinater ser man på avstanden fra origo og vinkelen som dannes med den positive x -aksen. Trykk på det grå feltet for å se en definisjon.
Et polarkoordinatsystem er et koordinatsystem hvor hvert punkt i et plan er bestemt ut ifra avstanden fra et gitt punkt (vanligvis origo ) og vinkel i forhold til X- aksen. I et vanlig kartesisk koordinatsystem blir punktene bestemt ut ifra avstanden til hver koordinatakse. Prinsippet i polarkoordinater er at man angir alle punkter ved . Vi måler vinkelen fra polaraksen og mot klokken, og vinkelen kan være negativ. Vi kan også bruke polarkoordinater i et rettvinklet ( kartesisk ) koordinatsystem. Vi tenker oss da x – aksen som polaraksen, med pol i origo ( ). Dette står ikke forklart noe sted i boken, så jeg er litt usikker på fremgangsmåte.
Vanligst brukt er rettvinklede ( kartesiske , parallelle, ortogonale) koordinatsystemer og polarkoordinater. I et rettvinklet koordinatsystem bestemmes beliggenheten av et punkt i planet ved . Type spherical_coordinate = cart2sph ( cartesian_coordinate ) for å konvertere kartesiske koordinatsystem til et sfærisk koordinere. Starter med Polar Koordinater 4. Punkter og vektorer kan skrives inn i kartesiske koordinater eller polarkoordianater (se avsnittet Tall og vinkler).
Merk: Store bokstaver angir punkter mens små bokstaver angir.

Merk: Du må bruke semikolon som skilletegn mellom de to koordinatene når du ønsker polarkoordinater. Hvis du ikke bruker symbolet for grader, . Kartesisk koordinater vs polarkoordinater I koordinatsystemet er et koordinatsystem et referansesystem hvor tall (eller koordinater) brukes til å bestemme posisjonen av et punkt eller et annet geometrisk element i rommet. Som vi ser, er kurven gitt på polarkoordinater , og vi må derfor gjøre om uttrykket til kartesiske koordinater.
Koordinatsystemene tillater at de geometriske problemene omdannes til et numerisk problem, som . Ь Э), kan vi ogs a beskrive funksjoner av to variable ved hjelp av polarkoordinater. Ю = (Ц ) istedenfor kartesiske koordinater. Dette gj0r en ved a sette (Ц ) = (Ц cos Ц sin ).





