Et polarkoordinatsystem er et koordinatsystem hvor hvert punkt i et plan er bestemt ut ifra avstanden fra et gitt punkt (vanligvis origo) og vinkel i forhold til X- aksen. I et vanlig kartesisk koordinatsystem blir punktene bestemt ut ifra avstanden til hver koordinatakse. Prinsippet i polarkoordinater er at man angir alle punkter ved . Dobbeltintegral – polarkoordinater. Flere resultater fra matematikk.
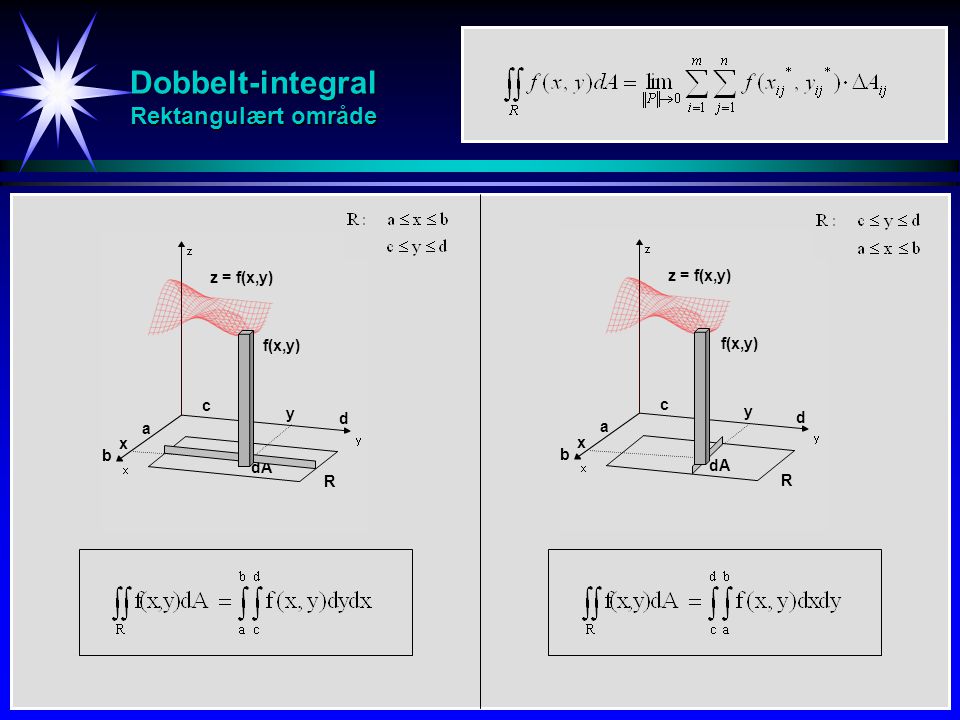
Volum og dobbeltintegral 10.

DOBBELTINTEGRALET I POLARKOORDINATER. Et svært viktig teknikk til ˚a beregne integraler i en varaibel, er substitusjon, som ogs˚a kan betraktes som et variabel skifte. Vi setter x = g(t) i integralet. Da blir dx = g (t)dt og de nye grensene er gitt ved . S er integrasjonsomr˚ adet beskrevet i vanlige koordinater, og R er inte- grasjonsomr˚adet beskrevet i polarkoordinater. Argumentet ovenfor er ikke et matematisk bevis siden det baserer seg p˚a.
Hvordan ser området D ut? A (ved hjelp av polarkoordinater ). Regn også ut integralet.
Hvis en flate er gitt som grafen til en funksjon f( x, y), kan det også ofte være naturlig å bruke polarkoordinater ( sylinderkoordinater) som parmetre. Areal med bruk av polarkoordinater. Enkle (x-enkle, y-enkle) og regulære integrasjonsområder. Itererte dobbeltintegraler. Bytte av integrasjonsrekkefølgen.
Uekte integraler for funksjoner med konstant fortegn. Middelverdien for en funksjon over et område i planet. Integrasjon i polarkoordinater. La R være det området som ligger innenfor den gitte sirkelen og til høyre for den gitte linjen. Vi skal benytte dobbeltintegral og polarkoordinater til å beregne arealet av området R. Vis ved hjelp av en figur i det kartesiske koordinatsystemet (xy-koordinatsystem).
Areal- og volumberegning ved dobbeltintegral , 224. Trippelintegral i sylinderkoordinater, 267. Anvendelser av trippelintegral . Kapittel Multiple integraler.
Innfør variabelskiftet x = au, y = bv og bruk teoremet for variabelytte i dobbeltinte- graler til˚a vise resultatet i pkt (b) ved˚a bruke at arealet av en sirkel med radius r = er π. Beregn arealet av sirkelen i punkt (c) ved ˚a transformere til polarkoordinater og utføre et dobbeltintegral over et rektangel. Kurveintegral, dobbeltintegral. Parametrisering av flater.

Gradient, konservative vektorfelt ,potensial. Funksjoner av to variable, nivåflater, partiell derivert, tangentplan, lineær approksimasjon. Kjerneregel , gradient og retningsderivert. FORMELSAMLING FOR BRUK VED EKSAMEN I. Vi skal nå definere et dobbelt integral på en funksjon f(x, y) over en bundet, ikke rektangulær region, som kan se ut som.
Noen integraler blir lettere å utføre hvis vi skifter til polar koordinater. Bruk polar koordinater til å finne arealet til regionen i x-y-planet som er bundet av sirkelen x.