Se en simpel måde at finde to vektorers determinant på. Tværvektoren er også vist i figuren med afsæt i punkt A. Vi bruger vores viden om vektorer i planen og sammenhængen mellem to vektorers prikprodukt og længden af den ene vektors projektion på . Areal af parallelogram udspændt af to vektorer og bestemmelse af parameter så arealet af. Helt overordnet defineres en vektor i rummet som en kombination af tre tal, man kalder for vektorens koordinatsæt.

I princippet er en vektor en pil og derfor har den både en længde og en retning. Hej jeg har lidt problemer med en vektor opgave. Håber der er nogen som vil FORKLARE opgaven!
Bestem areal af parallelogram ( vektor ) innlegg 25. Dette gør, at sin(v) vil være . Offline Worksheet (.zip). Michael Jensen — September 11:AM.
Viser hvordan man kan udregne arealet af et parallelogram uden trigonometriske funktioner.

Du skal logge ind for at skrive en note . Definition af krydsprodukt. This worksheet is also part of one or more other Books. Modifications will be visible in all these Books. Do you want to modify the original worksheet or create your own copy for this Book instead?
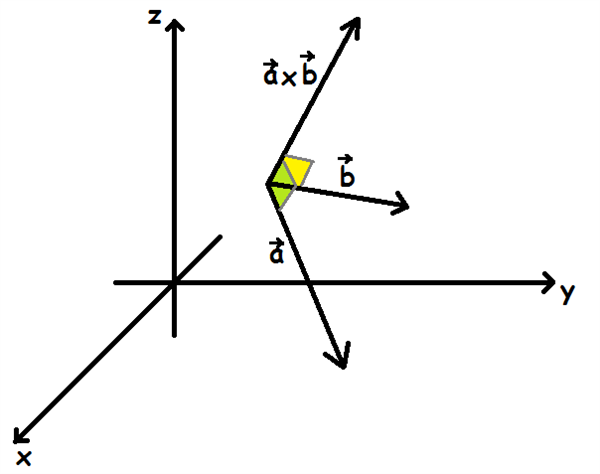
Ortogonale vektorer : Projektion af på : Krydsprodukt ( vektorprodukt ): hvor og og. Plan (ligning): normalvektor. Vinkel mellem linjer = vinkel mellem linjernes retningsvektorer. Der vil imidlertid være to vektorer som kan stå vinkelret på planet, hhv. Alt afhængig af hvilken rækkefølge man tager krydsproduktet i, vil man ende op med den ene . A = Altså er arealet af det udspændte parallelogram A Parallelogram = og dermed er arealet af en trekant ATrekant = . I Gympakken er der en række funktioner, der gør arbejdet med vektorer mere bekvemt: navn syntaks handling.
Beregner arealet af det parallelogram der er udspændt af og. Opgave og løses til sidst i opgaven ved brug af begreber, formler og sætninger fra de gennemgåede afsnit. Ellers siges orienteringen af.
Beregn således, at vektoren AB er vinkelret på vektoren a. I planen er givet punkterne A( 1- ), B( 3), C( 4) og D( k).
Bestem således at vektor CD er parallel med vektor.



