Regneregler: kommutative lov, associative lov, distributive love gælder(side 141). Stedvektor: har samme koordinater som punktet P. Vi lærer her formlen for at beregne den vinkelrette afstand mellem et punkt og en plan og viser et eksempel på udregningen. Vi lærer om skæringen og afstanden mellem to planer, samt planers relation ( afstand , skæring etc.) til vektorer.
Vi får forklaret, hvorfor man ikke kan tale om tværvektorer og derfor heller ikke en determinant, når man regner med 3D vektorer.
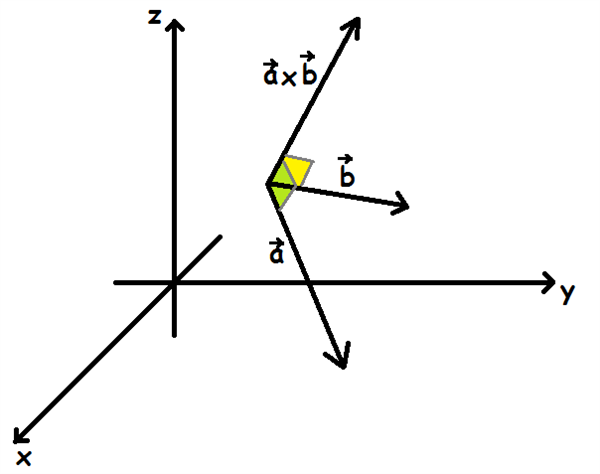
Lær at arbejde med linjer i rummet ved at bruge deres parameterfremstilling. De fleste begreber om vektorer fra 2D kan overføres direkte til 3D. Imidlertid gælder det ikke for tværvektor-begrebet. I rummet kan man nemlig ikke tale om at rotere en vektor 90º mod uret, da mod uret afhænger af, hvor man ser fra.
Der vil således være uendeligt mange måder at konstruere en vektor på, der står vinkelret . To linjer i rummet , som ikke er parallelle og som ikke skærer hinanden, er vindskæve. En retlinjet motorvej og en jerbane, der krydser motorvejen på en bro eller i en tunnel, er et eksempel på vindskæve linjer – der er ingen niveauoverskæring mellem dem.
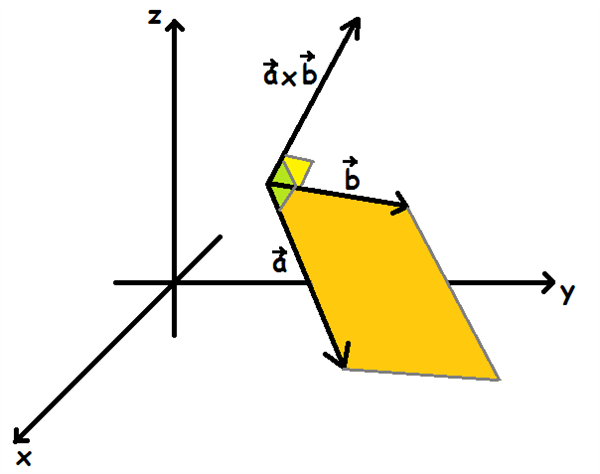
Projektion af vektor på vektor. Find punkt i den ene plan og så bruge n vektoren i den anden plan. Nu er du klar til at bruge formlen for afstanden mellem punkt og plan. Brit, Tina, Camilla V, Krydsprodukt, 5. Afstand fra punkt til plan, 8. Søkbæk, Ditlev, Maibritt, Kuglens ligning, 9. Thomas, Nanna, Jonas, Linier i rummet , 2. Når afstanden fra et punkt P til en linie l skal findes, er det den vinkelrette afstand mellem punktet og linjen der skal findes. Har vi retningsvektorer der ikke er parallelle og et kendt punkt, kan man opskrive en parameterfremstilling for planen.
Beviset for formlen minder om den tilsvarende formel for afstanden mellem et punkt til en linje i to dimensioner. Vinkel mellem vektorer. Parameterfremstilling for en ret linje i rummet.
I rummet har et punkt P(x,y,z) tre koordinater, som svarer til projektionen af P på de tre akser – helt på samme. Regneregler for skalarprodukt( kommunikativ, assosiativ, distributiv, ortogonalitet) 4. Vektor ud fra punkter 2.
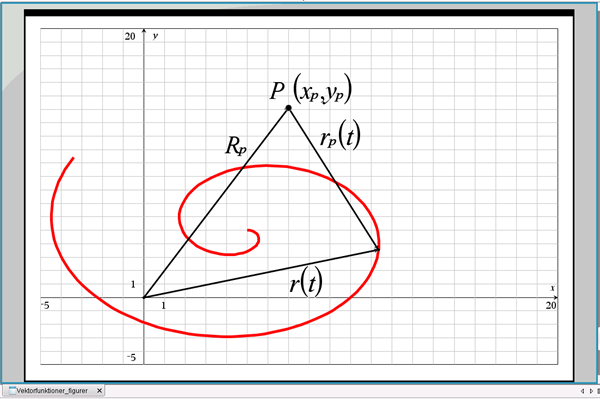
Dette gøres ved at indsætte koordinatsættet fra punkterne, i formelen. Nedenfor er sætningen og dens bevis for et todimensionelt, kartesisk koordinatsystem angivet. Når man har et punkt og en linje i rummet , så er der to fornuftige. Hvis ikke de skærer hinanden, hvad er så den kortest mulige afstand mellem dem?
Vi kan ved hjælp af en vektor finde afstanden mellem parallelle linjer. Den vektor vi så skal bruge for at finde afstanden mellem de linjer, det er den vektor som ligger vinkelret på vore linje og rammer vores vilkårlige punkt på den ene .